【C#】 Bスプライン曲線の実装

Bスプライン曲線を実装する必要があったので作ってみました（次数は3固定にしています）。使い方は以下の二通りを想定しています。

1. 制御点を指定して曲線を描く
2. 指定した点を通るような曲線を描く

まずはBスプライン曲線を描くクラスをBSplineとして実装します（BSplineクラスを動かすにはMathNet.NumericsをNuGetからインストールして下さい）。

// usingにMathNet.Numerics.LinearAlgebraを追加
using MathNet.Numerics.LinearAlgebra;

class BSpline
{
    // 次数
    private const int _degree = 3;
    // 制御点X
    private double[] _cxs;
    // 制御点Y
    private double[] _cys;
    // ノットベクトル
    private double[] _knotVector;

    public BSpline(double[] cxs, double[] cys)
    {
        _cxs = cxs;
        _cys = cys;
        _knotVector = CreateKnotVector(_degree, cxs.Length);
    }

    public void Interpolate(double t, out double x, out double y)
    {
        if (t < 0.0 || t > 1.0)
        {
            throw new ArgumentOutOfRangeException("t", "Argument must be 0 <= t <= 1.");
        }

        x = 0.0;
        y = 0.0;
        for (int i = 0; i < _cxs.Length; ++i)
        {
            Func<double, double> basis = Basis(i, _degree, _knotVector);
            double b = basis(t);
            x += _cxs[i] * b;
            y += _cys[i] * b;
        }
    }

    public void Interpolate(double[] ts, out double[] xs, out double[] ys)
    {
        xs = new double[ts.Length];
        ys = new double[xs.Length];
        for (int i = 0; i < ts.Length; ++i)
        {
            double x, y;
            Interpolate(ts[i], out x, out y);
            xs[i] = x;
            ys[i] = y;
        }
    }

    public static void Fit(double[] xs, double[] ys, out double[] cxs, out double[] cys)
    {
        if (xs.Length != ys.Length)
        {
            throw new ArgumentException("Length of xs and ys must be the same.");
        }
        if (xs.Length < _degree)
        {
            throw new ArgumentException("Length of xs and ys must be larger than " + _degree + ".");
        }

        int controlPointCount = Math.Max(xs.Length - 1, _degree);

        double[] chordLengthRatios = ComputeChordLengths(xs, ys);

        int n = controlPointCount - 1;
        double[] knotVector = CreateKnotVector(_degree, controlPointCount);

        var basisMatrix = new double[xs.Length, controlPointCount];
        for (int j = 0; j < basisMatrix.GetLength(0); ++j)
        {
            for (int i = 0; i < basisMatrix.GetLength(1); ++i)
            {
                basisMatrix[j, i] = Basis(i, _degree, knotVector)(chordLengthRatios[j]);
            }
        }
        var N = Matrix<double>.Build.DenseOfArray(basisMatrix);

        var pointMatrix = new double[xs.Length, 2];
        for (int i = 0; i < xs.Length; ++i)
        {
            pointMatrix[i, 0] = xs[i];
            pointMatrix[i, 1] = ys[i];
        }
        var D = Matrix<double>.Build.DenseOfArray(pointMatrix);

        var B = N.TransposeThisAndMultiply(N).Cholesky().Solve(N.TransposeThisAndMultiply(D));
        cxs = new double[controlPointCount];
        cys = new double[cxs.Length];
        for (int i = 0; i < cxs.Length; ++i)
        {
            cxs[i] = B[i, 0];
            cys[i] = B[i, 1];
        }
    }

    private static double[] ComputeChordLengths(double[] xs, double[] ys)
    {
        var chordLengths = new double[xs.Length];
        for (int i = 0; i < chordLengths.Length - 1; ++i)
        {
            chordLengths[i + 1] = Length(xs[i], ys[i], xs[i + 1], ys[i + 1]);
        }
        double lengthSum = chordLengths.Sum();
        var chordLengthRatios = new double[chordLengths.Length];
        for (int i = 0; i < chordLengthRatios.Length; ++i)
        {
            double sum = chordLengths.Take(i + 1).Sum();
            chordLengthRatios[i] = sum / lengthSum;
        }

        return chordLengthRatios;
    }

    private static double Length(double x1, double y1, double x2, double y2)
    {
        return Math.Sqrt(Math.Pow(x1 - x2, 2) + Math.Pow(y1 - y2, 2));
    }

    private static double[] CreateKnotVector(int degree, int controlPointCount)
    {
        int n = controlPointCount - 1;
        double maximumKnotValue = n - degree + 2;

        var knotVector = new List<double>();
        for (int i = 0; i < degree; ++i)
        {
            knotVector.Add(0.0);
        }
        for (int i = 1; i < maximumKnotValue; ++i)
        {
            knotVector.Add(i / maximumKnotValue);
        }
        for (int i = 0; i < degree; ++i)
        {
            knotVector.Add(1.0);
        }

        return knotVector.ToArray();
    }

    private static Func<double, double> Basis(int i, int k, double[] knotVector)
    {
        if (k < 1)
        {
            throw new ArgumentOutOfRangeException("k", "Argument k must be equal or more than 1.");
        }

        return (t) =>
        {
            // ノットベクトル値は0から1までしか受け付けない
            if ((t < 0.0) || (t > 1.0))
            {
                throw new ArgumentOutOfRangeException("t", "Argument must be between 0 and 1.");
            }

            if (k == 1)
            {
                if (t == 1.0)
                {
                    // 特殊ケース対応ロジック
                    if ((t >= knotVector[i]) && (t <= knotVector[i + 1]))
                    {
                        return 1.0;
                    }
                    else
                    {
                        return 0.0;
                    }
                }
                else
                {
                    // 通常ロジック
                    if ((t >= knotVector[i]) && (t < knotVector[i + 1]))
                    {
                        return 1.0;
                    }
                    else
                    {
                        return 0.0;
                    }
                }
            }
            else
            {
                double denominator1 = knotVector[i + k - 1] - knotVector[i];
                double n1;
                if (denominator1 == 0.0)
                {
                    n1 = 0.0;
                }
                else
                {
                    n1 = (t - knotVector[i]) / denominator1 * Basis(i, k - 1, knotVector)(t);
                }

                double denominator2 = knotVector[i + k] - knotVector[i + 1];
                double n2;
                if (denominator2 == 0.0)
                {
                    n2 = 0.0;
                }
                else
                {
                    n2 = (knotVector[i + k] - t) / denominator2 * Basis(i + 1, k - 1, knotVector)(t);
                }

                return n1 + n2;
            }
        };
    }
}

次にBSpineクラスの使い方ですが、まずは制御点を指定して曲線を描くサンプルです。

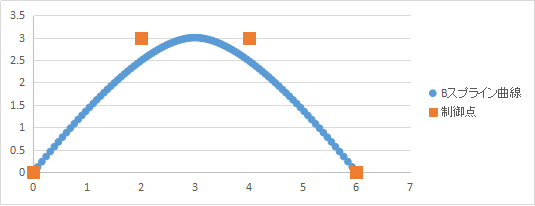
// 制御点
var cxs = new double[] { 0.0, 2.0, 4.0, 6.0 };
var cys = new double[] { 0.0, 3.0, 3.0, 0.0 };
// BSplineクラスの生成
var spline = new BSpline(cxs, cys);
var ts = Enumerable.Range(0, 101).Select(t => t / 100.0).ToArray();
double[] xs, ys;
spline.Interpolate(ts, out xs, out ys);

上記のcxs, cys, xs, ysを散布図で描くとこんな感じになります。

次に通って欲しい点を指定して曲線を描くサンプルです（フィッティング）。

// 指定した点を通るようなBスプライン曲線を描く制御点を計算する
var xs = new double[] { 0.0, 3.0 / 2.0, 3.0, 9.0 / 2.0, 6.0, 6.5, 6.0, 6.5 };
var ys = new double[] { 0.0, 2.0, 5.0 / 2.0, 2.0, 0.0, -2.0, -3.0, -5.0 };
double[] cxs, cys;
BSpline.Fit(xs, ys, out cxs, out cys);
// Bスプラインクラスの生成
var spline = new BSpline(cxs, cys);
var ts = Enumerable.Range(0, 101).Select(t => t / 100.0).ToArray();
double[] axs, ays;
spline.Interpolate(ts, out axs, out ays);

上記のcxs, cys, axs, aysを散布図で描くとこんな感じになります。

ちなみに上記プログラムは以下の本を参考にして実装しました。ベジェ曲線から始まり順を追って丁寧に説明されているので良書と思います。

An Introduction to NURBS: With Historical Perspective (The Morgan Kaufmann Series in Computer Graphics)